DAFTAR ISI
HALAMAN JUDUL
...........................................................................................................
i
KATA PENGANTAR
........................................................................................................
ii
DAFTAR ISI
......................................................................................................................
iii
BAB I PENDAHULUAN
1.1 Latar Belakang
....................................................................................................
1
1.2 Rumusan masalah
...............................................................................................
1
1.3 Batasan masalah
..................................................................................................
1
1.4 Tujuan
.................................................................................................................
2
1.5 Manfaat ...............................................................................................................
2
BAB II PEMBAHASAN
2.1 Sejarah Integral .................................................................................................
3
2.2 Integral Tentu ....................................................................................................
3
2.3 Aplikasi Integral
dalam Biologi ........................................................................
4
2.4 Polutan dan Ekosistem
......................................................................................
4
2.5 Aplikasi Integral
dalam Menghitung Polutan ................................................... 5
BAB III PENUTUP
3.1 Kesimpulan
......................................................................................................
7
BAB I
PENDAHULUAN
1.1 Latar Belakang
Integral merupakan invers atau kebalikan dari
diferensial. Integral memiliki banyak kegunaan dalam berbagai bidang, misalnya
bidang ekonomi, astronomi, permodelan dalam ilmu biologi, ilmu fisika, dan ilmu
kimia. Prinsip-prinsip integral diformulasikan oleh Isaac Newton dan Gottfried
Leibniz pada abad 17 dengan memanfaatkan hubungan erat yang ada antara anti
turunan dan integral tentu, yaitu suatu hubungan yang memungkinkan kita untuk
menghitung secara mudah nilai yang sebenarnya dari banyak integral tentu tanpa
perlu memakai jumlah Riemann.
Pada dasarnya integral terbagi atas dua macam, yaitu
integral tentu dan integral tak tentu. Integral tentu adalah suatu integral
yang dibatasi oleh suatu nilai tertentu yang biasa disebut sebagai batas atas
dan batas bawah. Integral ini biasanya digunakan untuk mencari luas suatu area
maupun volume suatu benda putar.
Namun dalam kenyataannya konsep integral bisa
diaplikasikan dalam berbagai bidang termasuk ilmu biologi antara lain :
mengukur volume darah yang mengalir dalam pembuluh darah, mengubah energy
menjadi gerak otot, mengukur banyak polutan yang memasuki ekosistem dan lain
sebagainya. Dalam makalah ini saya lebih menspesifikkan perhitungan integral
untuk mengukur banyak polutan yang memasuki ekosistem.
Jumlah Polutan ini sudah cukup mengkhawatirkan bagi
ekosistem di lingkungan kita. Bukan hanya di Negara kita, di berbagai Negara
pun kerusakan lingkungan yang diakibatkan oleh polutan tersebut sudah begitu
tinggi. Penggunaan bahan-bahan kimia, limbah tekstil, asap kendaraan, dan
sampah-sampah plastik yang tidak dapat terurai oleh tanah menjadi penyebab
semakin tidak seimbangnya lingkungan. Oleh karena itu aplikasi perhitungan
jumlah polutan yang masuk dalam ekosistem ini dengan menerapkan konsep integral
tentu merupakan langkah awal untuk mengetahui seberapa banyak dampak polutan
yang dihasilkan oleh salah satu pabrik. Sehingga mampu meminimalisir kerusakan
lingkungan yang akan terjadi.
1.2 Rumusan Masalah
Rumusan masalah dalam makalah ini yaitu, bagaimana
konsep Integral Tentu jika diaplikasikan ke dalam bidang biologi khususnya
untuk menghitung banyak polutan yang memasuki ekositem.
1.3 Batasan Masalah
Dalam makalah ini saya lebih menspesifikkan
perhitungan integral untuk mengukur banyak polutan yang memasuki ekosistem.
1.4 Tujuan
Tujuan penulisan makalah ini yaitu untuk memberikan
penjelasan konsep integral tentu yang diaplikasikan ke dalam ilmu biologi
khususnya untuk mengukur banyak polutan yang memasuki ekosistem.
1.4 Manfaat
Manfaat
penulisan makalah ini yaitu agar mahasiswa mengetahui konsep integral tentu
dapat diaplikasikan ke berbagai bidang salah satunya bidang Biologi.
BAB II
PEMBAHASAN
2.1 Sejarah Integral
Georg
Friedrich Bernhard Riemann (1826 – 1866) merupakan seorang matematikawan yang
pada kala itu merupakan mahasiswa dari salah satu universitas Gottingen yang
merupakan pusat matematikawan dunia. Riemann-lah yang memberi kita definisi
modern tentang integral tentu, yaitu tentang jumlah Riemann sebagai jumlah luas
siku empat.
Konsep
dasar integral berbatas (integral tentu) atau integral Riemann sesungguhnya
telah diperkenalkan oleh Archimedes dalam abad ketiga sebelum Masehi dalam
usahanya menghitung luas daerah bidang datar yang dibatasi oleh kurva-kurva
kontinu. Namun, pada abad ke-17 Newton dan Liebniz menemukan teorema yang dalam
banyak hal mampu menghitung integral tertentu dengan lebih ringkas tanpa
melalui pelimitan jumlah Riemann. Teorema ini diberi nama Teorema Dasar
Kalkulus (TDK) dan berfungsi sebagai jembatan antara kalkulus diferensial dan
kalkulus integral.
2.2 Integral Tentu
Integral
merupakan invers atau kebalikan dari diferensial. Pada dasarnya integral
terbagi atas dua macam, yaitu integral tentu dan integral tak tentu. Integral
tentu adalah suatu integral yang dibatasi oleh suatu nilai tertentu yang biasa
disebut sebagai batas atas dan batas bawah. Integral ini biasanya digunakan
untuk mencari luas suatu area. Bentuk umum dari integral tentu adalah :
Integral tentu terbagi atas dua macam, yaitu integral
tentu sebagai limit jumlah Riemann dan integral berdasarkan teorema dasar
kalkulus.
Integral tentu dapat digunakan untuk mendefinisikan
dan menghitung panjang, luas, volume yang memuat juga konsep volume benda
putar, usaha/kerja, momen dan pusat massa. Untuk menyelesaikan persoalan pada
konsep integral tentu maka muncul teknik pengintegralan yang bersifat integral
parsial dan dengan menggunakan aturan rantai maka muncul aturan substitusi yang
mencakup juga substitusi trigonometri.
Pendiferensialan integral tentu
menurut Newton dan Leibniz yang dikemukakan dalam
Teorema
A :
Teorema B :
2.3 Aplikasi Integral
dalam Biologi
Integral
tentu dapat digunakan untuk menghitung luas. Ini tidak mengherankan oleh karena
integral tersebut memang diciptakan untuk keperluan tersebut. Akan tetapi
integral tersebut dapat digunakan untuk banyak persoalan lainnya. Hampir tiap
besaran yang dapat dianggap sebagai hasil pemotongan sesuatu menjadi bagian-bagian
lebih kecil, aproksimasi tiap bagian, penjumlahan dan pengambilan limit apabila
tiap bagian mengecil, dapat diartikan sebagai suatu integral.
Sejauh
ini belum banyak contoh penggunaan integral tentu di bidang Biologi yang dapat
dibahas. Hal ini, mungkin karena jenis fungsi yang banyak digunakan di bidang
biologi masih sedikit dibicarakan.
2.4 Polutan dalam
Ekosistem
Polusi
atau pencemaran lingkungan adalah masuknya atau dimasukkannya makhluk hidup,zat
energi,dan atau komponen lain ke dalam lingkungan oleh kegiatan manusia atau
oleh proses alam sehingga kualitas lingkungan turun sampai ke tingkat tertentu
menyebabkan lingkungan menjadi kurang atau tidak dapat berfungsi lagi sesuai
dengan peruntukannya. (Undang-Undang Pokok Pengelolaan Lingkungan Hidup Nomor 4
Tahun 1982)
Zat
atau bahan yang menyebabkan polusi disebut dengan polutan. Suatu zat yang
disebut sebagai polutan, apabila keberadaannya dapat menyebabkan kerugian
terhadap makhluk hidup. Kategori suatu zat disebut polutan apabila jumlahnya melebihi
keadaan normal, berada pada waktu dan tempat yang tidak tepat. Polutan dapat
bersifat merusak sementara dan merusak dalam jangka waktu panjang.
Jenis
polusi yang banyak dirasakan saat ini, salah satunya polusi udara. Polutan yang
menyebabkan polusi udara ini terbagi menjadi polutan primer dan polutan
sekunder. Polutan primer adalah substansi pencemar yang ditimbulkan langsung
dari sumber polusi udara. Contohnya, karbon monoksida yang langsung dihasilkan
dari pembakaran. Pencemar sekunder adalah substansi pencemar yang terbentuk
dari reaksi pencemar-pencemar primer di atmosfer. Contohnya, pembentukan ozon
dalam smog fotokimia.
Adanya
polutan dalam suatu lingkungan (ekosistem), dalam waktu singkat, dapat
menyebabkan perubahan biokimiawi suatu organisme. Selanjutnya perubahan
tersebut dapat mempengaruhi perubahan fisiologis dan respon organisme,
perubahan populasi, komposisi komunitas, dan fungsi ekosistem.
Berdasarkan
Polutan (Bahan Pencemar),polusi dapat dikelompokkan menjadi polusi karena bahan
fisik, kimia, dan biologi.
a.
Polusi karena
Bahan Fisik
Polusi ini disebabkan bahan pencemar fisik berupa
bahan-bahan yang sukar hancur, seperti alumunium, fisik, kaca, dan karet
sintetis.
b.
Polusi karena
Bahan kimia
Polusi ini disebabkan bahan pencemar kimia, seperti
zat radoaktif, logam (Hg,Pb, As, Cr dan Cd), detergen, minyak, pupuk organik,
dan pestisida.
c.
Polusi karena
Bahan Biologi
Polusi ini disebabkan pencemar biologi berupa
mikroorganisme, misalnya salmonella thyposa, Escherichia coli, dan Entamoeba
coli.
2.5 Aplikasi Integral
dalam Menghitung Polutan
Banyaknya
polutan yang memasuki suatu ekosistem dapat bervariasi menurut waktu tergantung
pada berbagai faktor. Misalkan, banyaknya limbah suatu pabrik yang dialirkan ke
Danau pembuangan dapat bertambah jika produksi pabrik meningkat atau alat
penyaring limbah pabrik menjadi tidak efisien.
Berikut
merupakan contoh aplikasi integral tentu dengan kasus menghitung jumlah polutan
yang masuk ke dalam ekosistem :
Contoh Kasus :
jika
banyaknya limbah yang terkumpul di suatu ekosistem setelah satuan waktu dapat
kita misalkan t, maka laju populasi pada ekosistem itu sama dengan  , sehingga banyaknya
limbah yang terkumpul di dalam ekosistem dari waktu 𝑡=𝑎 sampai 𝑡=𝑏 menjadi :
, sehingga banyaknya
limbah yang terkumpul di dalam ekosistem dari waktu 𝑡=𝑎 sampai 𝑡=𝑏 menjadi :
Jika
suatu pabrik mengganti saringan udara setiap 90 hari dan t hari, setelah
penggantian saringan udara banyaknya sulfur dioksida yang terlepas ke udara
adalah satuan berat per hari,
maka banyaknya polutan adalah :
satuan berat per hari,
maka banyaknya polutan adalah :
 satuan berat per hari,
maka banyaknya polutan adalah :
satuan berat per hari,
maka banyaknya polutan adalah :
Jadi
banyak limbah yang terkumpul dalam ekosistem adalah 4500 satuan berat.
BAB III
PENUTUP
PENUTUP
3.1 Kesimpulan
Berdasarkan
kasus diatas diperoleh kesimpulan bahwa konsep kalkulus integral, khususnya
integral tentu dapat diaplikasikan ke berbagai bidang termasuk biologi. Dengan
menggunakan Teorema Dasar Kalkulus konsep integral dapat digunakan untuk
menghitung jumlah polutan yang masuk ke dalam ekosistem.





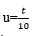

No comments:
Post a Comment